Attributed as the 8th Wonder of the World by Einstein, Compound Interest can be our number 1 ally in the quest for financial independence. The analogy of a snowball rolling down a mountain could never be more apt. The longer and further it travels, the bigger it becomes. Now apply this to your finances. The longer we put our money to work for us, the greater they will become.

What is Compound Interest?
Compound interest is focused on the act of saving money. As you save, the value of your savings not only grow due to the balance you add, but also the interest earned. Compound interest refers to the interest earned on the interest itself. Each year your savings and the interest remain in your account, the greater the return. To return to our snowball analogy. As your savings compound each year, they grow at a faster rate. The longer you leave your savings untouched, the faster they should grow.
Compounding Example
Lets say we save £1000 today. Theroetically we earn 10% on this balance in the next 12 months. Our interest value equals £100 and our total investments/savings not add to £1100. At the end of year 2, with a further 10% growth, we now have an interest value of £110. Our total value of savings/investments becomes £1210.
Consider the above increase from £1000 to £1210 with the addition of no further capital. The following year, under the same interest % assumptions, there would be an increase of £121 on top of the £1210.
Compounding Rate – When is interest compounded?
Depending on your saving channel, the frequency at which interest is accumulated will change. Some interest is calculated daily, but it is more common to be annual, quarterly or monthly. This will determine the rate of compound interest. The interest rate and distribution schedule will be outlined in the documentation you are provided when setting up your savings channel.
When Compound Interest Works Against you
As those focused on early retirement or financial Independence, we naturally fall into the category of savers. With this in mind, compound interest works for us. Our money is put to work! The concept also works in equal measure against those who take on debt and the interest we may pay on it. Accruing debt through credit cards or loans, you are paying back the interest on the loan and the interest on the interest.
Paying off debt must become a priority. A small amount of debt left unpaid can grow rapidly in the same manner as savings grow to benefit us.
Compound Interest on Investments
Our investments operate in a fairly similar manner to savings and the interest earned within such accounts. Fixed Rate ISAs may give a determined rate annually as may Bonds. The rate of return from such options may seem quite low. For example the current interest rate on a cash ISA sits somewhere around the 0.5% annually mark.
For those looking to outpace inflation and create healthy annualised returns over a long period of time, the answer may be index funds. In such funds, not only are dividends paid annually. The added benefit is that we are also wholly focused on the growth of the fund.
Example: If we assume today we have £1000 to invest for the next 25 years. At an interest rate of 0.5%, our total return will be £1,132.80. Compare that with an annualised return of 8%, our investments total £6,848.48.
While you can never be guaranteed positive returns with investing, over a long term horizon, investing should massively outperform saving. The only guarantee is that if you don’t save, you’ll earn nothing.
The Importance of Time in the Market
If we consider the snowball once more. The longer it runs, the larger it becomes. Even if you can only invest a little early in life, it’s advisable to begin investing in your 20s. Time in the market makes a huge difference to the amount you need to save.
Joe (20) and Sarah (35) are brother and sister. They’ve both recently found out about financial independence and are intent on retiring at 57. They decide to invest in the same index fund. Over the course of their investing horizon they make 10% annual gains in their investments. Both have an initial lump sum £10,000 to put into their investment. The only difference is time.
Scenario 1: Joe is invested for 37 years. His £10,000 compounds to £340,039.49 without addition of new funds to the investment each year.
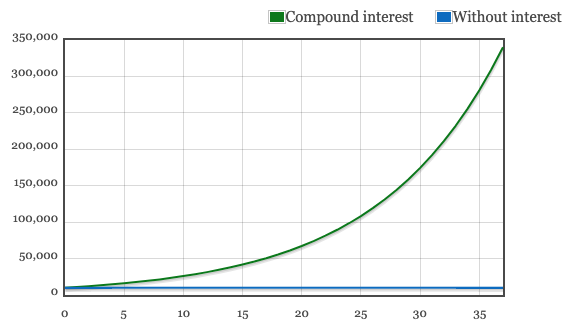
Scenario 2: Sarah with her shorter 22 year investment horizons see her future value much lower at £81,402.75.
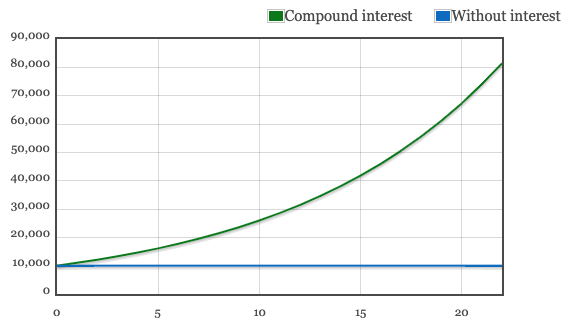
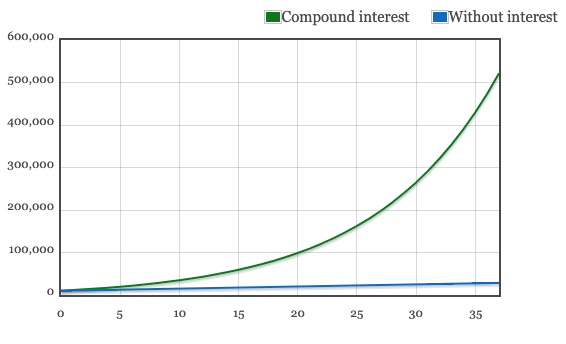
Now consider each have a financial independence goal of £500,000.
Scenario 1: To reach his goal, Joe would have to add £500 each year to his investments. A total investment amount of £28,500 would achieve £521,561.20.
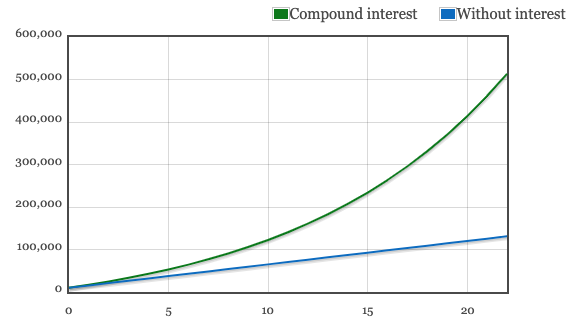
Scenario 2: With a shorter investing timeframe, Sarah will need to contribute a greater annual amount to her investments. If she wants to retire with more than £500,000 at age 57. Using the values noted above, Sarah would need to add £5,500 per year to investments to achieve a future value of £513,389.38. A total of £131,000 would be required.
Am I too late to start saving for retirement?
It’s obvious that the best time to start investing for your financial independence was 10 years ago. The second best time is today. You may not financially be where you hoped, but with a conscious effort there are very easy steps to start tipping the scales in your favour. The very first step is always to consider your spending and see if possible to reduce costs. This will have a huge effect on the value you need to become financially independent. Check out our How to Budget Money Effectively article here – https://foundered.co.uk/how-to-budget-money/.
Compound Interest Calculator
There are a huge array of compound interest calculators available online, however one of the easiest to use belongs to incredible personal finance blog Monevator. The screenshots from the examples above are output from the https://monevator.com/compound-interest-calculator/. The calculator does not of course count for inflation, so reduce your expected interest rate by the value of the expected inflation rate for a truer figure.
What is compound interest?
Compound interest refers to the snowballing effect that happens when the interest from your investments grows on top of your interest over time. This exponential increase is compounding for your benefit.
How is compound interest benefit me?
If you invest £100 and gain an interest rate of 10%. After year 1, the value of your investments is £110. After a second year invested. The interest not only grows on the original amount, but also the interest you gained in year 1. So £110+10% = £121. In year 3 your interest would be calculated by adding 10% to the £121 balance, totalling £133.1.


